Paxos算法

Posted on 2017-03-23 | Edited on 2019-03-25 | In 算法

Paxos算法是莱斯利·兰伯特(Leslie Lamport)于1990年提出的一种基于消息传递且具有高度容错性的一致性算法，是目前公认的解决分布式一致性问题最有效的算法之一。

两篇经典论文

我主要针对《从Paxos到Zookeeper分布式一致性原理与实现
》书里第二章的内容和《Paxos Made Simple》论文的原文，对Paxos算法进行详细的阐述。

Java8的lambda和默认方法

Posted on 2017-03-20 | Edited on 2019-03-25 | In Java

Labmda

Lambda的基本语法是

(parameters) -> expression

或者

(parameters) -> {expression;}

这里讨论一种异常情况。假设你用与Runnable同样的签名声明了一个函数接口，我们称之为Task。

interface Task {
    void exexute();
}

public static void doSomething(Runnable r) {r.run();}
public static void doSomething(Task t) {t.execute();}

如果我们用以前的匿名类是没问题的:

doSomething(new Task() {
    void execute() {
        System.out.println("Danger danger!!");
    }
})

但是将这种匿名类转换为Lambda表达式时，就导致了一种晦涩的方法调用，因为Runnable和Task都是合法的目标类型：

1	doSomething(() -> System.out.println("Danger danger!!"));

这时候编译器会报一个编译的异常，Ambigulous method call，这时候需要对Task尝试使用显示的类型转换来解决这种模棱两可的情况:

1	doSomething((Task)() -> System.out.println("Danger danger!!"));

接口默认方法

概念

Java8引入了一种新的机制。Java8中的接口现在支持在声明方法的同事提供实现。通过两种方式可以完成这种操作。

Java8允许在接口内声明静态方法。
Java8引入了一个新功能，叫默认方法。

在新的Collection接口中的stream和List接口中的sort都是这样的。定义如下：

default Stream<E> stream() {
    return StreamSupport.stream(spliterator(), false);
}

@SuppressWarnings({"unchecked", "rawtypes"})
default void sort(Comparator<? super E> c) {
    Object[] a = this.toArray();
    Arrays.sort(a, (Comparator) c);
    ListIterator<E> i = this.listIterator();
    for (Object e : a) {
        i.next();
        i.set((E) e);
    }
}

默认方法设计的目的是为了解决向接口添加方法。

Java8中的抽象类和抽象接口

那么既然接口也能实现方法，抽象类也能实现方法，区别如下：

一个类只能继承一个抽象类，但是一个类可以实现多个接口。
一个抽象类可以通过实例变量(字段)保存一个通用状态，而接口是不能有实例变量的。

解决冲突的规则

先看下面的场景

public interface A {
    default void hello() {
        System.out.println("Hello from A");
    }
}

public interface B {
    default void hello() {
        System.out.println("Hello from B");
    }
}

public class C implements B, A {
    public static void main(String[] args) {
        new C().hello();
    }
}

###解决问题的三条规则
如果一个类使用相同的函数前面从多个地方继承了方法，通过三条规则可以进行判断。

类中的方法优先级最高。类或父类中声明的方法的优先级高于任何声明为默认方法的优先级。
如果无法依据第一条进行判断，那么子接口的优先级更高：函数前面相同时，优先选择拥有最具体实现的默认方法的接口，即如果B继承了A，那么B就比A更加具体。
最好，如果还是无法判断，继承了多个接口的类必须通过显示覆盖和调用期望的方法，显示地选择使用哪一个默认方法的实现。

Java8引入了一种新的语法X.super.m()，其中X是你希望调用的m方法所在的父接口。

使用自动机来索引1,600,000,000个键

Posted on 2017-03-18 | Edited on 2019-03-25 | In 数据结构

本文翻译自Index 1,600,000,000 Keys with Automata and Rust，所以标题也直译过来。

有限状态机(FSM, finite state machine)可以用来紧密地存储有序集合和有序键值对，并且可以实现快速搜索。本文中，我会表明怎样用FSM来作为数据结构存储这样的数据。

FSM作为数据结构

FSM是一个状态的集合和状态转移的集合。一个起始状态，0个或多个结束状态。一个FSM在同一时间只有一个状态。

FSM非常常见，并且可以用来描述一系列过程。比如我家猫咪Cauchy一天的日常生活:

Cauchy的一天

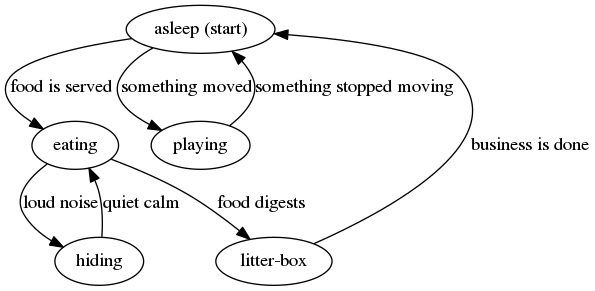
里面有一些”asleep”或者”eating”的状态，一些转移”food is served”, “something moved”。这里没有结束状态，如果结束了，那真是太恐怖了！

FSM近似的表达了现实中的情况。Cauchy不可能同时吃饭和睡觉，这跟FSM中同一时刻只有一个状态是一样的。并且，从一个状态转移到另一个状态需要外部环境的一个输出。需要睡觉，可能是因为”吃饱了”, “累了”等等。不管他睡得多死，”听到外面的声音”，它总会醒过来。

有序集合

有序集合里的键按照字典序排序。典型的应用是二叉查找树和B树。无序集合，典型应用就是哈希表。这里，我们先描述一个确定无环有限状态接收器(deterministic acyclic finite state acceptor)，即FSA。

一个FSA需要满足以下条件：

确定性的。给定已给输入，最多只能转移到一个状态。
无环的。不能反序遍历。
接收器。FSA可以接收一系列特定的输入。

那么，怎么用这些特性来表示一个集合呢。诀窍在于，key作为FSA的状态转移。这样，给定一个输入key，我们可以知道这个key这个key是否在FSA中。

假设一个集合，只有一个key”jul”。FSA就像下面这样：

集合1

这时候如果问FSA，是否包含”jul”。处理顺序如下：

给定j，FSA状态从0变为1.
给定u，FSA状态从1变为2.
给定l，FSA状态从2变为3.

输入结束，这时候判断一下FSA是否处在final状态(图中用双圈表示)，表明jul确实在set中。

这时候如果问FSA，是否包含”jun”。处理顺序如下：

给定j，FSA状态从0变为1.
给定u，FSA状态从1变为2.
给定l，FSA不动，处理结束。

FSA不动，因为状态2只接收’l’的转移，但是当前输入为’n’。因此处理结束，也表明集合中不包含”jun”。

这时候如果问FSA，是否包含”ju”。处理顺序如下：

给定j，FSA状态从0变为1.
给定u，FSA状态从1变为2.

判断一下，此时是否处于final状态。

值得注意的是，判断一个key是否存在，受限于key的长度，而不是set的大小。

下面把key”mar”添加到FSA中去，这时候FSA的表现如下：

集合2

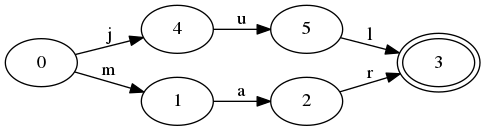
FSA变得稍微复杂一点，状态0可以有两个转移。如果起始输入mar，它会先转移到1状态。

还有一个需要注意的是，状态3被jul和mar两个key共享。即，状态3可以由l和r转移过来。这种共享的方式，可以用更少的空间保存更多的信息。

如果再加入jun，FSA表现如下：

集合3

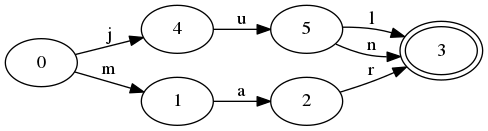
看到变化了么？只有一点点变化。FSA看起来和之前的几乎没什么区别。唯一变化的地方在状态5多了一个转移。FSA其实没有新增状态节点，因为jun和jul共享了前缀ju

下面展示一个更复杂的FSA，包含三个key，october，november，december。

集合3

因为有相同的后缀ber，在FSA中只需要编码一次就行了。两个key有更大的相同的后缀，ember。

在介绍FST之前，我们先看看，如何来遍历FSA中所有的key呢？

为了阐述这个过程，还用一个之前的一个简单的图，有三个key，jul，jun和mar。

集合3

遍历方式如下：

初始化状态0
移动到状态4，把j添加到key中
移动到状态5，把u添加到key中
移动到状态3，把l添加到key中，输出jul
返回状态5，把key中的l抛弃掉
移动到状态3，把n添加到key中，输出jun
返回状态5，把key中的n抛弃掉
返回状态4，把key中的u抛弃掉
返回状态0，把key中的j抛弃掉
移动到状态1，把m添加到key中
移动到状态2，把a添加到key中
移动到状态3，把r添加到key中，输出mar

这个算法直接应用一个栈存储访问过的状态，和一个栈存储相应的转移。时间复杂度为O(n)，空间复杂度O(k)，k是set中最长的键的大小。

有序map

和有序集合类似，只是多了一个输出。有序map常用在二叉查找树和b树，无序map就是hashtbale。这里我们介绍一个deterministic acyclic finite state transducer，确定无环有限状态转移器，FST。

FST满足以下特性：

确定性。
无环。
一个转移器。给定一系列输入，会输出一个值。当且仅当输入会达到FST的final状态。

FST和FSA很像，但是对于一个key，FSA只回答了”yer or no”，FST不仅回答”yes or no”，还好返回和这个key相关的一个值。

在有序集合中，只需要把key保存在转移时。但是在这里，还需返回与key对于的value。

一种方法是，在每次转移的时候添加一些值。当输入序列在状态之间转移的时候，输出序列也在慢慢增加。

还是看一个简单的例子吧。map中只包含一个数据jul，对应的value为7:

map1

这和上面的集合差不多，只是在第一个转移状态j之后多了一个相关联的输出7.另外的转移u和l对应的输出都是0，所以图中就不显示了.

如果要判断，FST中是否存在key”jul”，并且需要对应的返回值，处理过程如下：

初始化value为0
给定输入j,FST从状态0转移到1，value+7
给定输入u，FST从状态1转移到2，value+0
给定输入l，FST从状态2转移到3，value+0

输入结束，状态3为final状态，因此key存在，value为7

下面把k-v,”mar 3”添加到FST中

map2

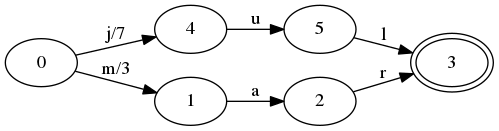
在起始节点，多了一个新的转移m，对应输出为3.如果我们查询jul，那么应该和上面是一样的处理过程。

继续，当添加一个有相同前缀的key，会发生什么呢？
添加key jun，value 6

map3

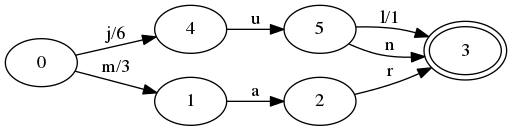
在状态5和状态3之间添加了一个转移n。但是还有另外两个变化

0->4转移j输入对应输出从7变成了6.
5->3转移l输入对应输出从0变成了1.

这个变化之后们可以正确查询jun和jul，并且返回正确的值。

这种key的属性确保了，即使共享前缀，对于每一个key，然后只有一个唯一的路径可以贯穿整个machine。因此，每个key也有唯一的value。我们要做的就是怎么把这些输出放在转移中去。

其实不仅可以共享前缀，还可以共享后缀。对于两个key tuesday和thursday，分别对于输出3和5.

map后缀

这两个key有相同的前缀t，相同的后缀sday，按照图里的方式可以保证输出的正确性。

这里在描述输出的时候，其实有一点局限，如果输出不是整形。确实，在FST里用做输出的类型必须满足以下特性：

加法
减法
取前缀（对于整数来说就是min）

构建

Trie树构建

trie树，前缀树。和FSA的区别在于，FSA可以共享前缀和后缀。对于键mon，tues，thus来说，FSA如下：

FSA

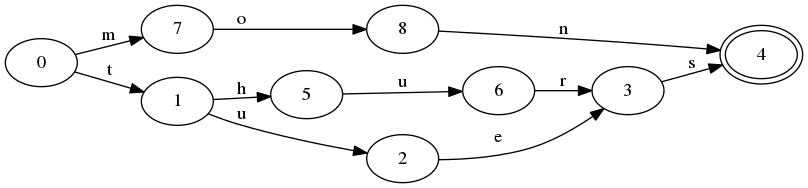
而trie树只共享前缀，如下：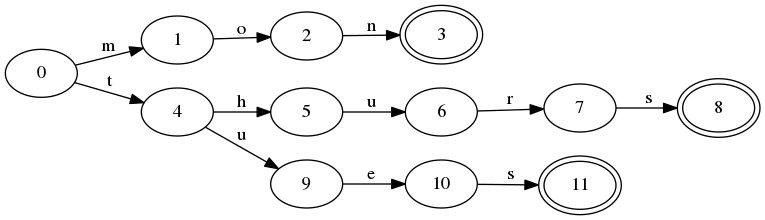
Trie

构建trie树很直接的，对于一个给定的输入，只需要去看看有没有相同的前缀。直到找出相同的前缀，余下的直接转移到一个final状态就可以了。

FSA构建

FSA和trie的区别在于，共享后缀。因此一个FSA的空间会比trie少很多，但是构建起来却更复杂，因此我们如果按照key的字典序插入的话，会好很多，还是用图片来说明。

对于三个key，mon，tues和thurs。按照字典序，插入顺序mon，thurs和tues。先插入mon：

插入mon

下面插入thurs:

插入thurs

插入thurs的时候，会导致之前的mon被冻结。当FSA中一部分被冻结的时候，我们知道，它以后再也不会被更改了。因为按照字典序排序的，后面的key肯定都是大于等于thurs的。因此不会和mon有相同前缀的key插入了。蓝色的state代表被冻结住，以后不会被更改但是可以被复用。

虚线的状态表示thurs还没有被真正加入到FSA中去，下面插入tues：

插入tues

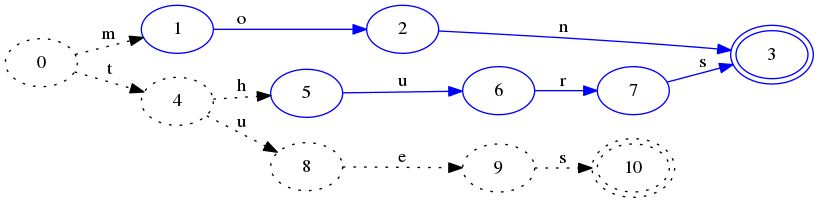
在这一步里，我们可以确定hurs会被冻住。因为将会不会有和它有相同前缀的词插入进来了。因为thurs和mon可以有相同的final state了。

这里状态4仍然是虚线，因为还不能确定t开头的key还有没有了。如果下面插入zon：

插入zon

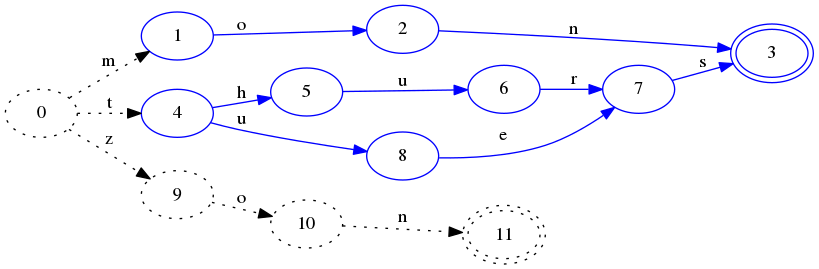
看到，这时状态4已经被冻住了，因为不会在有t开头的key出现了，另外thurs和tues有一个共同的后缀s，因此状态7和状态9被合并了。

最后，在结束操作以后，把FSA的最后一部分冻住，一个完整的没有重复的结构如下：

完成的FSA

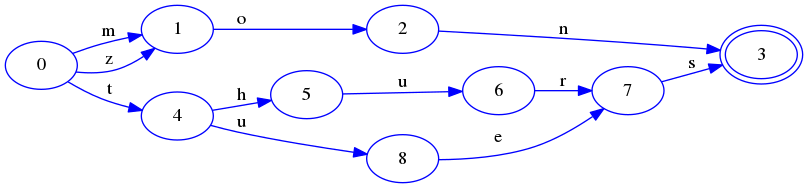
因为mon和zon有相同的后缀，因此它们除了第一个状态转移不一样，剩下的可以重复利用。

FST构建

下面快速说一下FST构建，插入键值对 mon-2，tues-3，thurs-5.

直接上图，插入mon-2

FST1

对于第一步，我们也可以这样分配输出的值

FST1-alt

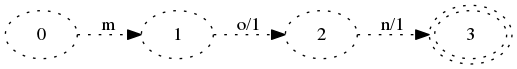
其实这样也是可以的，但是在算法上来说，把输出放在靠近初始状态的地方，代码写起来更简单。

插入thurs-5

FST2

插入tues-3

FST3

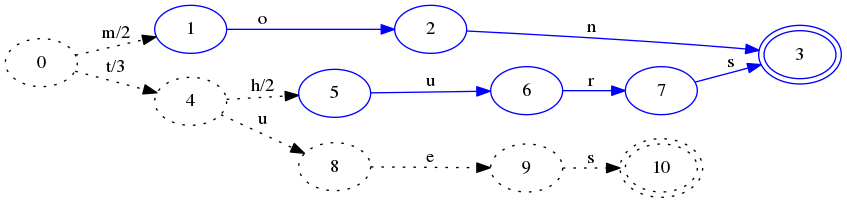
在把状态0-4之间的输出从5变为3的之后，需要把4之后所有的输出全部加2，除了新添加的key，这样就可以保持输出的平衡。

下面插入一个tye-99

FST4

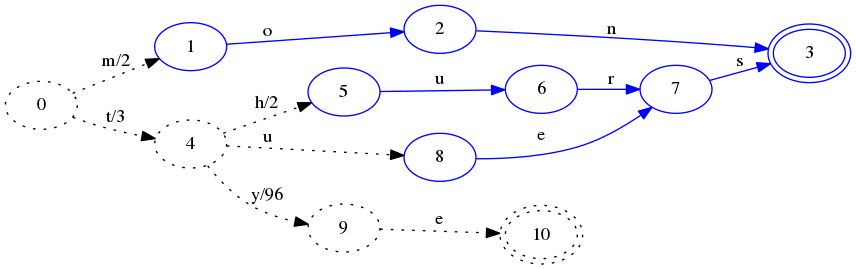
最后的完全形态

FST5

Lucene索引内存结构

Posted on 2017-03-10 | Edited on 2019-03-25 | In Solr

Lucene索引在内存中的结构主要分为三个部分: field, term, docId，具体如下。

Field在内存中的组织结构

field->fileposition，域名对应在文件中的偏移量，TreeMap<String,Long> fields = new TreeMap<>();.

Google Java风格指南

Posted on 2017-01-19 | Edited on 2019-03-25 | In Java

转载一篇Google的Java编程风格指南，自己手打一遍，也算是阅读，顺带添加以下原文和自己的理解。

参考文章

原文

1 简介 Introduction

This document serves as the complete definition of Google’s coding standards for source code in the Java™ Programming Language. A Java source file is described as being in Google Style if and only if it adheres to the rules herein.

Like other programming style guides, the issues covered span not only aesthetic issues of formatting, but other types of conventions or coding standards as well. However, this document focuses primarily on the hard-and-fast rules that we follow universally, and avoids giving advice that isn’t clearly enforceable (whether by human or tool).

windows查看端口占用

Posted on 2017-01-12 | Edited on 2019-03-25 | In 杂

运行命令行或者cmd+r
执行命令netstat -ano查看端口占用情况
查看被占用端口对应的PID，输入命令：netstat -ano|findstr “49157”
继续输入tasklist|findstr “2720”，回车，查看是哪个进程或者程序占用了2720端口，结果是：svchost.exe
或者打开任务管理器ctrl + shift + esc 查找对应PID 然后kill掉

Solr6.3快速入门

Posted on 2017-01-07 | Edited on 2019-03-25 | In Solr

刚入门做Java，做Solr一个多月了，其实还是了解点皮毛，今天正好看了官方的pdf，从入门开始说起吧。

平时开发是在Windows环境下的，就说说Windows吧

Redis设计与实现-第8章-对象

Posted on 2017-01-06 | Edited on 2019-03-25 | In Redis

前面陆续介绍了Redis用到的所有主要数据结构。但是Redis并没有直接使用这些数据结构来实现键值对数据库，而是给予这些数据结构创建了一个对象系统，这个系统包含字符串对象、列表对象、哈希对象、集合对象和有序集合对象这五种类型的对象，每种对象都用到了至少一种我们前面所介绍的数据结构。

好处是：

可以根据对象的类型来判断一个对象是否可以执行给定的命令
针对不同的使用场景来为对象设置多种不同的数据结构实现，从而优化对象在不同场景下的使用效率

Redis的对象系统实现了基于引用计数的的内存回收机制；还通过引用技术技术实现了对象共享机制，可以让多个数据库键共享同一个对象来节约内存。

Redis对象带有访问时间记录信息，该信息可以同于计算数据库键的空转时长，在服务器启用了maxmemory功能的情况下，空转时长较大的那些键可能会有点被服务器删除。

Redis设计与实现-第7章-压缩列表

Posted on 2017-01-05 | Edited on 2019-03-25 | In Redis

压缩列表(ziplist)是列表键和哈希键的底层实现之一。当一个列表键只包含少量列表项，并且每个列表项要么就是小整数值，要么就是长度比较段的字符串，那么Redis就会使用压缩列表来做列表键的底层实现。

redis> RPUSH lst 1 3 5 10086 "hello" "world"
(integer) 6

redis> OBJECT ENCODING lst
"ziplist"

Redis设计与实现-第6章-整数集合

Posted on 2017-01-05 | Edited on 2019-03-25 | In Redis

整数集合（intset）是集合键的底层实现之一，当一个集合只包含整数值元素，并且这个集合的元素数量不多时，Redis就会使用整数集合作为集合键的底层实现。

redis> SADD numbers 1 3 5 7 9
(integer) 5

redis> OBJECT ENCODING numbers
"intset"

整数集合的实现

整数集合是Redis用于保存整数值的集合抽象数据结构，它可以保存类型为int16_t、int32_t或者int64_t的整数值，并且保证集合中不会出现重复元素。

蒋士正

音浪太强不晃会被撞到地上